Last week, I’ve played a little bit with the Netflix prize dataset and NC-ISC. The results are amazingly better than the current state of the art.
Short version
Netflix dataset contains ratings of movies by user. We try to predict unseen good ratings (a few ratings are kept aside in a separate dataset, and we try to see if we can predict that a given user would have rated those particular movies).
I’ve compared state-of-the-art results with my method, NC-ISC. With the best settings, I can predict 24% of the unseen ratings in the first 50 results, compared to 19% for the current best methods. Considering the fact that a non personalized prediction, based on popularity only, gives a 10% score, what we achieved is a 55% improvement over the current state of the art.
This is a huge gain.
And it could be applied to other recommendation problems : music, jobs, social network, products in e-commerce and social shopping, etc.
A bit of context
The Netflix Prize was an open competition held in 2009. The dataset consist of 100M ratings (1-5) given by 400K+ user on 17K+ movies. The original goal was to predict “unseen” ratings with the highest possible accuracy. The measure used was the RMSE (root mean square error) on the hidden ratings.
The RMSE, however, is a very incomplete evaluation measure (and also it cannot be estimated on the results of NC-ISC, which is one of the reason we haven’t spent much time to compare our results with the state of the art). Indeed, the common task for a recommender system is not to predict the rating you would give a given movie, but to provide you a list of K movies that you could potentially like.
As a result, more and more effort has been put on the so-called top-K recommender task, and as a side effect on learning to rank instead of learning to rate.
I’ve stumbled recently on an interesting paper : Alternating Least Squares for Personalized Ranking by Gabor Takacs and Domonkos Tikk, from RecSys 2012 (which has been covered here), and found myself happy to find a paper with results I could compare to (often, either the metric, or the dataset is at odds with what I can produce/access).
The experiment
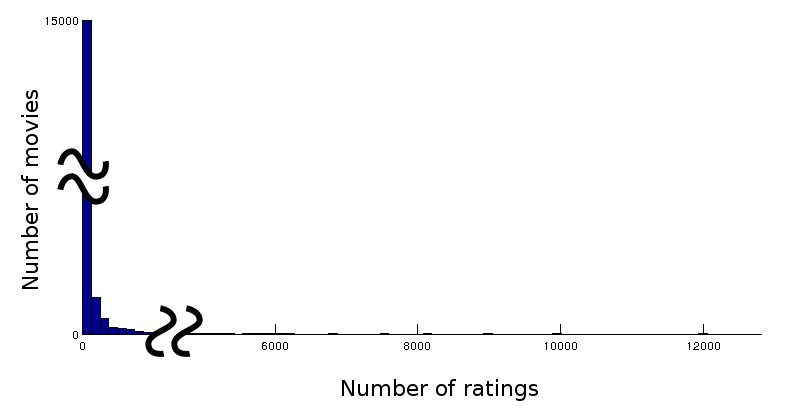
So I ran NC-ISC on the same dataset they used in the paper (just keep the top ratings), which reduce the train dataset to 22M ratings and the probe to 400K ratings. At first the results were very disappointing. The main reason for this is that NC-ISC inherently discards any bias on popularity. And the fact is, ranking Movies is a very popularity-biased problem (below we can see that 15000 movies have very few ratings in the test set, while a few movies have 12000 ratings) :
However, while NC-ISC cannot perform rating prediction natively, and discards popularity in both its learning and its ranking, it’s quite easy to put popularity back into the learning, and back into the ranking. Putting it back in the ranking simply means to multiply the score produced by NC-ISC by each movie popularity. Putting popularity back into the learning means decreasing the unbiasing factor in NC-ISC.
The results
And here we come (I’ve added my results as an overlay to the original paper figure). Just a disclaimer : while I’ve reproduced results from the popularity baseline, I didn’t have the time to check the implicit ALS results (I’ve got an implementation here in Octave that take hours to run), so I’m not 100% confident I haven’t missed something in the reproduction of the experiment.
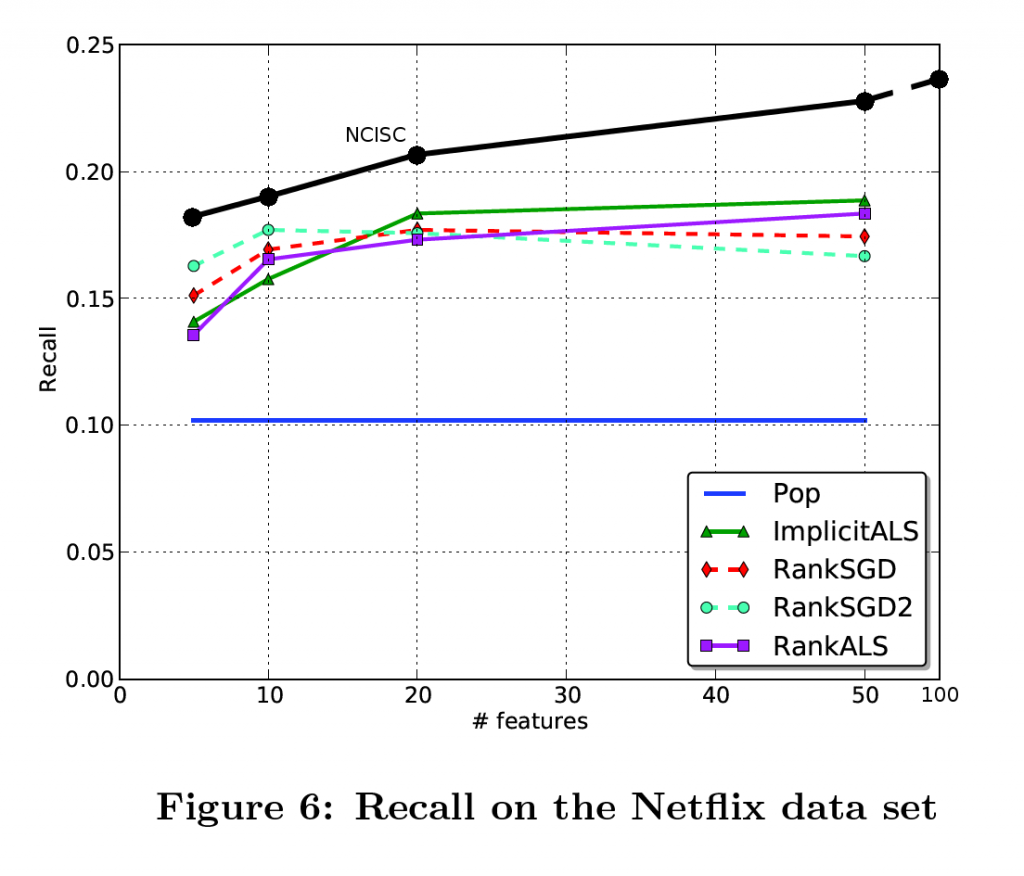
I’ve added a mark for 100 features, which wasn’t in the original paper, probably since there results tended to stop improving.
Performance
A short note about NCISC performance versus ImplicitALS, RankALS and RankSGD. First, while SGD takes on average 30 iterations to converge, ALS and NCISC takes between 5 and 10 iterations.
Regarding iteration time, while Takacs and Tikk give their timings for Y!Music data, I could only work top Netflix ratings dataset. However, the two datasets have approximately the same number of ratings (22M) and approximately the same total number of elements (17700 + 480189 = 497889 for Netflix, 249012+296111= 545123 for Y!Music).
Finally, I’ve run my unoptimized algorithm using 1 core of a Core i7 980 (cpumark score 8823 for 6 cores), while they have used 1 core of a Xeon E5405 (2894 for 4 cores) to run their unoptimized RankALS and ImplicitALS and optimized RankSGD algorithms. The rescaling factor to account for the processor difference is thus exactly 2 (!)
Here are my rescaled timings and the original timings of the other methods (remember it’s not an optimized version, though):
| method |
#5 |
#10 |
#20 |
#50 |
#100 |
| NC-ISC |
1 |
2 |
4 |
10 |
25 |
| ImplicitALS |
82 |
102 |
152 |
428 |
1404 |
| RankALS |
167 |
190 |
243 |
482 |
1181 |
| RankSGD |
21 |
25 |
30 |
42 |
65 |
| RankSGD2 |
26 |
32 |
40 |
61 |
102 |
Time (seconds) per iteration for various # of features.
Speedup range from x3 to x167 per iteration (for SGD you should account for the increased number of iterations required). I’ve generally observed that my optimized implementations of NC-ISC run 10 to 20 times faster than my Matlab implementation.


